一、介绍
在CTR预估问题的发展初期,使用最多的方法就是逻辑回归(LR),LR使用了Sigmoid变换将函数值映射到0~1区间,映射后的函数值就是CTR的预估值。
LR属于线性模型,容易并行化,可以轻松处理上亿条数据,但是学习能力十分有限,需要大量的特征工程来增加模型的学习能力。但大量的特征工程耗时耗力同时并不一定会带来效果提升。因此,如何自动发现有效的特征、特征组合,弥补人工经验不足,缩短LR特征实验周期,是亟需解决的问题。
Facebook 2014年的文章介绍了通过GBDT解决LR的特征组合问题,随后Kaggle竞赛也有实践此思路,GBDT与LR融合开始引起了业界关注。
在介绍这个模型之前,我们先来介绍两个问题:
1)为什么要使用集成的决策树模型,而不是单棵的决策树模型:一棵树的表达能力很弱,不足以表达多个有区分性的特征组合,多棵树的表达能力更强一些。可以更好的发现有效的特征和特征组合
2)为什么建树采用GBDT而非RF:RF也是多棵树,但从效果上有实践证明不如GBDT。且GBDT前面的树,特征分裂主要体现对多数样本有区分度的特征;后面的树,主要体现的是经过前N颗树,残差仍然较大的少数样本。优先选用在整体上有区分度的特征,再选用针对少数样本有区分度的特征,思路更加合理,这应该也是用GBDT的原因。
二、小知识
1.Normalized Cross-Entropy(NE)
2.lgb.Dataset 使用Dataset构建数据到lgb中。
示例代码:
import lightgbm as lgb import numpy as np # 训练数据,500个样本,10个维度 train_data = np.random.rand(500, 10) # 构建二分类数据 label = np.random.randint(2, size=500) # 放入到dataset中 train = lgb.Dataset(train_data, label=label) 还可以指定 feature names(特征名称)和 categorical features(分类特征): train_data = lgb.Dataset(data, label=label, feature_name=['c1', 'c2', 'c3'], categorical_feature=['c3'])
3.lgb_eval 创建验证数据
在LightGBM中,验证数据应该与训练数据一致(格式一致)。
4.lgb.train
lgb参数的参数可以看这里:https://blog.csdn.net/qq_23069955/article/details/80611701
LGB(机器学习模板):https://blog.csdn.net/sunshunli/article/details/82830969
主流机器学习模型模板代码+经验分享[xgb, lgb, Keras, LR]:https://blog.csdn.net/leyounger/article/details/78667538
上面这个人的博客可以看看。
XGBoost Plotting API以及GBDT组合特征实践:https://blog.csdn.net/zhangf666/article/details/70183788
5.num_trees
print(np.array(y_pred).shape)
print(y_pred[:1])的输出结果:
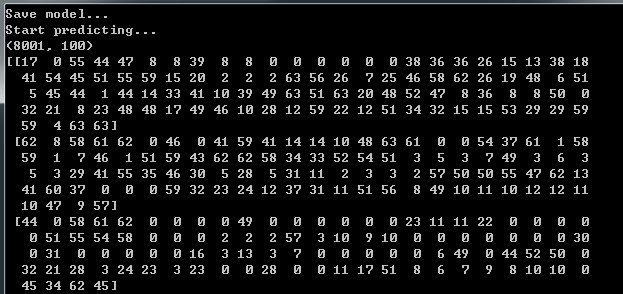
这里的100的和代码中的'num_trees': 100 相对应。8001和总共有8001个样本对应。
6.temp
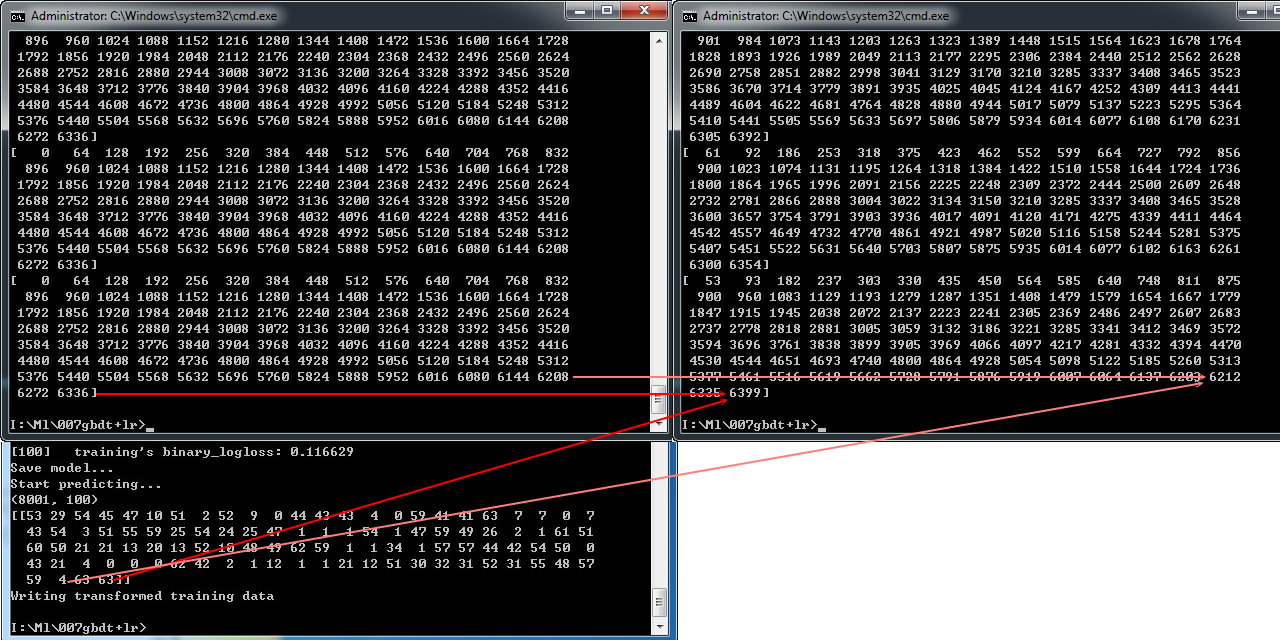
附:LightGBM 中文文档
https://lightgbm.apachecn.org/#/
7.lm.predict_proba
可参考: 集成学习将数据投影到高维建模 https://www.jianshu.com/p/08baad546bac
8.lm = LogisticRegression(penalty='l2',C=0.05)
penalty:惩罚项,str类型,可选参数为l1和l2,默认为l2。用于指定惩罚项中使用的规范。newton-cg、sag和lbfgs求解算法只支持L2规范。L1G规范假设的是模型的参数满足拉普拉斯分布,L2假设的模型参数满足高斯分布,所谓的范式就是加上对参数的约束,使得模型更不会过拟合(overfit),但是如果要说是不是加了约束就会好,这个没有人能回答,只能说,加约束的情况下,理论上应该可以获得泛化能力更强的结果。
c:正则化系数λ的倒数,float类型,默认为1.0。必须是正浮点型数。像SVM一样,越小的数值表示越强的正则化。
更多参数看:LogisticRegression - 参数说明 https://blog.csdn.net/kingzone_2008/article/details/81067036
9.transformed_training_matrix[i][temp]
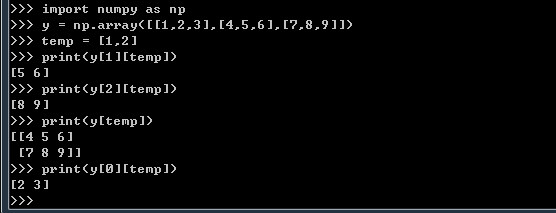
这段代码:
print(transformed_training_matrix[2]) #结果为(8001, 6400)
for i in range(0, len(y_pred)):
temp = np.arange(len(y_pred[0])) * num_leaf + np.array(y_pred[i])
print(temp)
transformed_training_matrix[i][temp] += 1 #意思是将temp中数据对应的列的值加上1
print(len(transformed_training_matrix[i]))
结果:

3.面板回归与截面回归
解释1:
在多因子选股里面有两个非常著名的名词,一个叫面板回归,一个叫截面回归。
面板回归,输入的是全部股票的多个因子,输入可以理解为,每一行都是一个股票的多因子,然后无次序的把所有股票都扔进去。然后输入还是一长段时间,输出为一段时间后的收益率等等。
截面回归:则是输入全部股票的单个因子,输出收益率等等。
解释2:
时间序列指的是用于数据分析的数据的一种数据形态。严格上的话指没有个体差异,而有时间差异的一系列数据。举个例子的话就是2000年到2010年中国每年的gdp,个体只有一个,中国,而时间的话有2000年到2010年11年,形成一组时间序列数据。
与时间序列数据对应的概念是横截面数据和面板数据。
横截面数据指有个体差而没有时间差的数据,比如2010年世界发达国家各国的gdp。
面板数据则指有时间差也有个体差的数据,比如2000年到2010年世界发达国家各国的gdp。
而回归分析(regression)是一种数据分析的手法,针对不同的数据形态和想要研究的问题,有不同的合适的回归分析手法。比如说题主说的ar,其全称其实是autoregression,即自回归,是回归分析中的一种模型。
回归分析中又有三大参数估计方法,即最小二乘估计(ols: ordinary least squares),广义矩估计(gmm: general moment method)和最大似然估计(mle: maximum likelihood estimate)。大部分模型在计算估计参数的时候用的就是这三种方法中的一种。
4.对数据的假设

二、train.csv
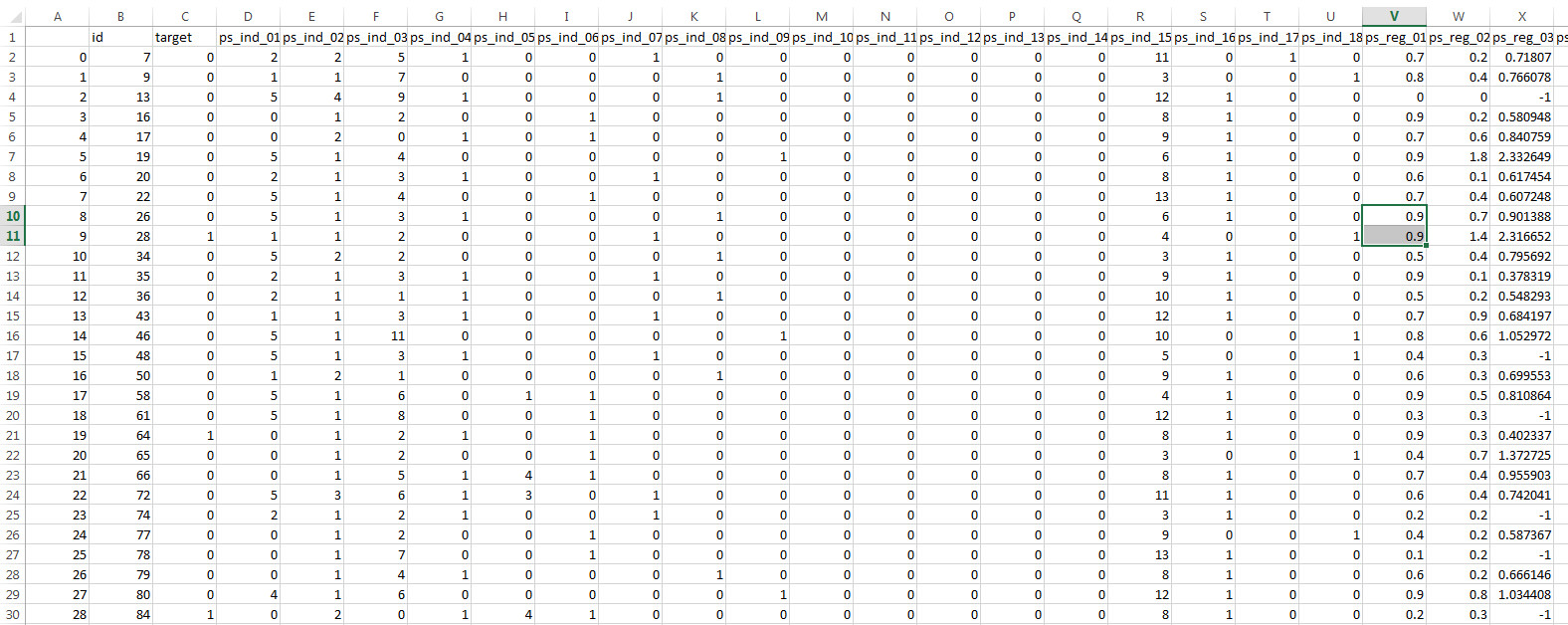
三、结果
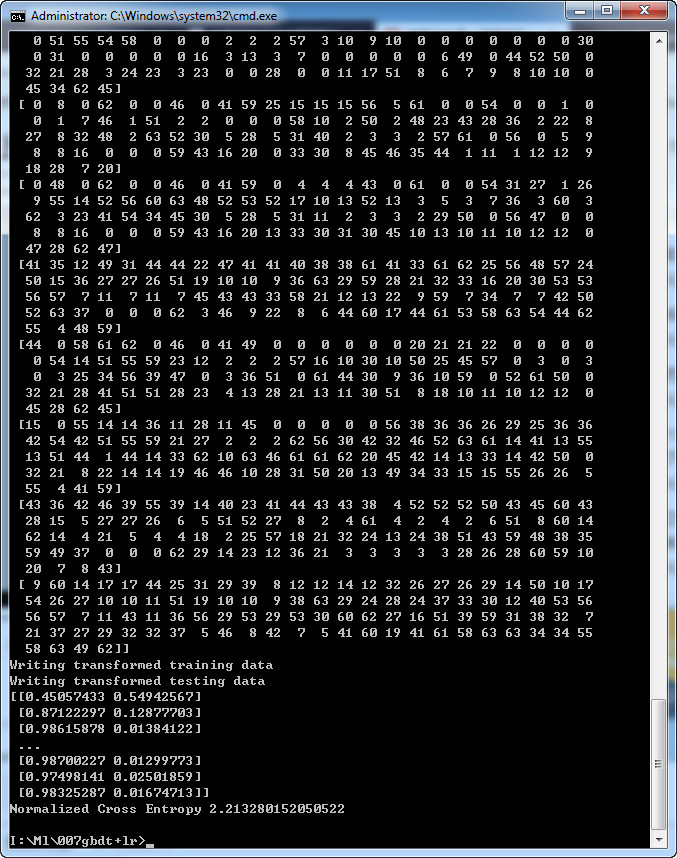
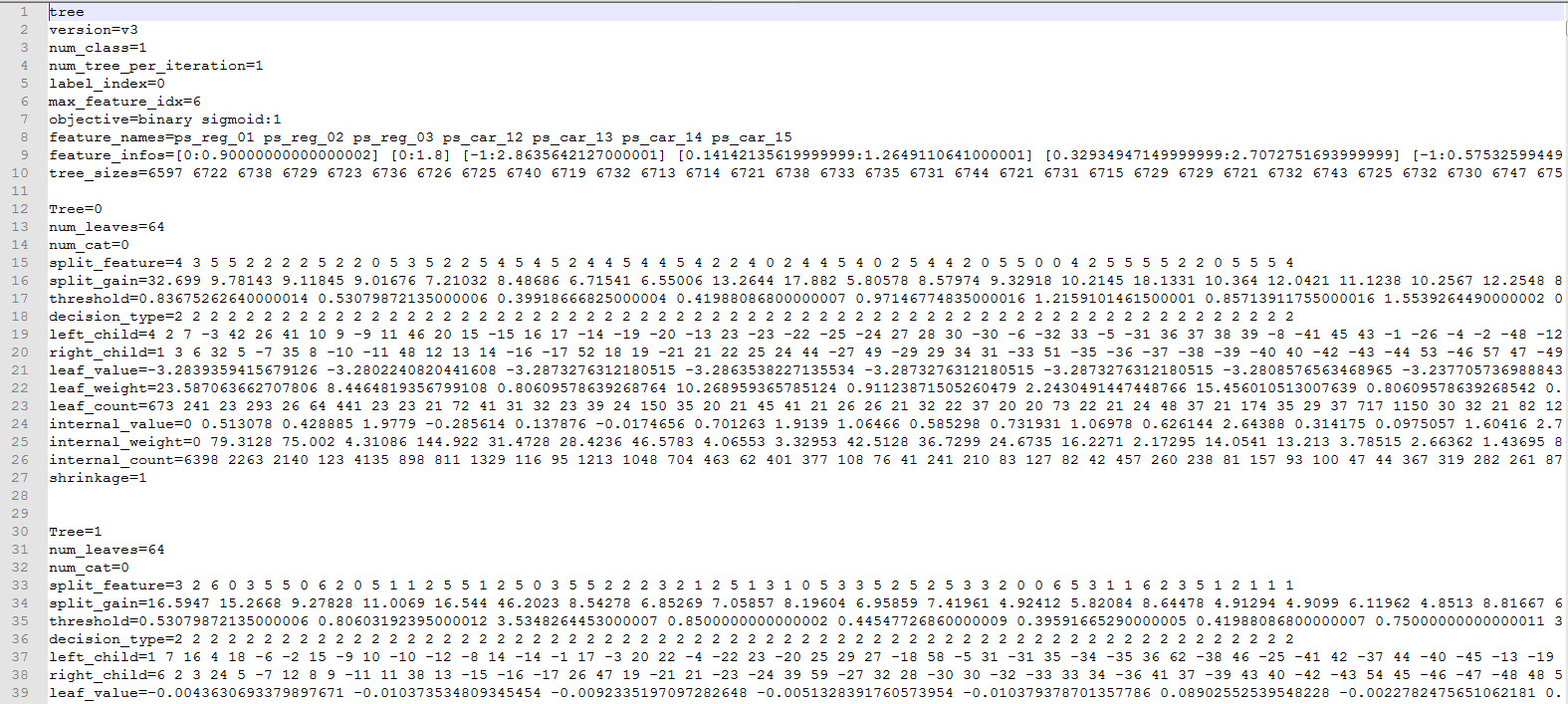
model.txt
四、代码
import lightgbm as lgb
import pandas as pd
import numpy as np
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import LogisticRegression
print('Load data...')
df_train = pd.read_csv('data/train.csv')
df_test = pd.read_csv('data/test.csv')
NUMERIC_COLS = [
"ps_reg_01", "ps_reg_02", "ps_reg_03",
"ps_car_12", "ps_car_13", "ps_car_14", "ps_car_15",
]
print(df_test.head(10))
y_train = df_train['target'] # training label
y_test = df_test['target'] # testing label
X_train = df_train[NUMERIC_COLS] # training dataset
X_test = df_test[NUMERIC_COLS] # testing dataset
# create dataset for lightgbm
lgb_train = lgb.Dataset(X_train, y_train)
lgb_eval = lgb.Dataset(X_test, y_test, reference=lgb_train)
params = {
'task': 'train',
'boosting_type': 'gbdt',
'objective': 'binary', # 比如要完成预测用户是否买单行为,所以是binary,不买是0,购买是1
'metric': {'binary_logloss'}, # 评判指标
'num_leaves': 64, # 大会更准,但可能过拟合
'num_trees': 100,
'learning_rate': 0.01, # 学习率
'feature_fraction': 0.9, # 防止过拟合
'bagging_fraction': 0.8, # 防止过拟合
'bagging_freq': 5, # 防止过拟合
'verbose': 0
}
# number of leaves,will be used in feature transformation
num_leaf = 64
print('Start training...')
# train
gbm = lgb.train(params,
lgb_train,
num_boost_round=100,
valid_sets=lgb_train)
print('Save model...')
# save model to file
gbm.save_model('model.txt')
print('Start predicting...')
# predict and get data on leaves, training data
# 当设置pred_leaf=True的时候, 这时就会输出每个样本在所有树中的叶子节点。
y_pred = gbm.predict(X_train, pred_leaf=True)
print(np.array(y_pred).shape) #输出结果为(8001, 100)这样的形式
print(y_pred[:10])
print('Writing transformed training data')
transformed_training_matrix = np.zeros([len(y_pred), len(y_pred[0]) * num_leaf],
dtype=np.int64) # N * num_tress * num_leafs,生成一个8001,100*64的np
#print(len(y_pred)) #结果为8100
#print(len(y_pred[0])) #结果为100
#print(transformed_training_matrix.shape) #结果为(8001, 6400)
for i in range(0, len(y_pred)):
temp = np.arange(len(y_pred[0])) * num_leaf + np.array(y_pred[i]) ##这段代码的意思是生成一个1-100的列表*64+每个样本在所有树中的叶子节点
transformed_training_matrix[i][temp] += 1
y_pred = gbm.predict(X_test, pred_leaf=True)
print('Writing transformed testing data')
transformed_testing_matrix = np.zeros([len(y_pred), len(y_pred
lm = LogisticRegression(penalty='l2',C=0.05) # logestic model construction
lm.fit(transformed_training_matrix,y_train) # fitting the data
y_pred_test = lm.predict_proba(transformed_testing_matrix) # Give the probabilty on each label
print(y_pred_test)
NE = (-1) / len(y_pred_test) * sum(((1+y_test)/2 * np.log(y_pred_test[:,1]) + (1-y_test)/2 * np.log(1 - y_pred_test[:,1])))
print("Normalized Cross Entropy " + str(NE))
可参考:
1.https://zhuanlan.zhihu.com/p/37522339
2.https://www.toutiao.com/i6644852565341110791/
3.Facebook经典模型LR+GBDT理论与实践:https://blog.csdn.net/u010352603/article/details/80681100#21-normalized-cross-entropyne

