我当初关注到RSRS,是因为当时无论是做股票和ETF的,还是做期货CTA或者是大饼的圈子,都有不少人提到它,它被提及的频次仅次于MACD,说是网红指标也毫不为过,好奇心被勾起来了,就去细细研究和向大神们学习呗,于是乎才有了当时那篇ETF轮动的文章。
闲白说完,现在开始入活~~~
1.RSRS的来源和思想
RSRS指标的全称是“阻力支撑相对强度(Resistance Support Relative Strength)”,它诞生于光大证券
在2017年劳动节发布的金工研报
《基于阻力支撑相对强度的市场择时》,这个系列的研报有好几篇,目录放在文末参考资料那里了,想看的小伙伴在公Z号【量化君也】后台回复暗号『RSRS』便可以保存下载阅读。

具体的渊源和概念可以参照原版研报,如果只想听个大体思路的话,暂且听我之前的闲话唠一唠。
刚开始做交易的时候,总会听到一些"专家"预测点位,说大盘的阻力位在哪,说某只股票的支撑位在哪,各有各的理由,众说纷纭,但是预测的点位也是"一千个人眼里有一千个哈姆莱特",不知道谁说的对。
后来慢慢发现,无论是在开发股票策略还是CTA策略,都不知不觉的使用了阻力和支撑的概念,比如说在做趋势策略之时,突破上轨做多,突破下轨做空,这个上下轨其实就类似于阻力线和支撑线,向上突破了阻力线后,广阔天地,大有可为,就开多仓,向下突破支撑线后,失去靠山,一泻千里,则开空仓或平仓。

有的时候,阻力线和支撑线并不是分开的两条线,也可以是一条线,这条线既可以是阻力线,也可以是支撑线。
就拿很多萌新入门常用的单均线策略来说,价格上穿20日均线做多,价格下穿20日均线做空,在这里,这根20日均线既是阻力线也是支撑线。价格在均线下方之时,均线便是阻力线,向上突破则做多,反之,价格在均线上方,此时均线则化身为支撑线,当价格失去支撑时则做空或平仓。
那问题来了,怎么找到阻力位和支撑位呢?听网上那些“专家”的预测吗?当然不是啦~
其实我们每天看K线图,“公认”的阻力和支撑就蕴含在里面,那就是K线的最高价和最低价,不要脸地说,这两个价格是经过万千交易者充分交易后的博弈结果,所有的成交价格都包含在了最高价和最低价形成的空间里,在最高价这条阻力线之下,在最低价这条支撑线之上。当然了,光用1天的最高价和最低价当然不行,可以用序列值。
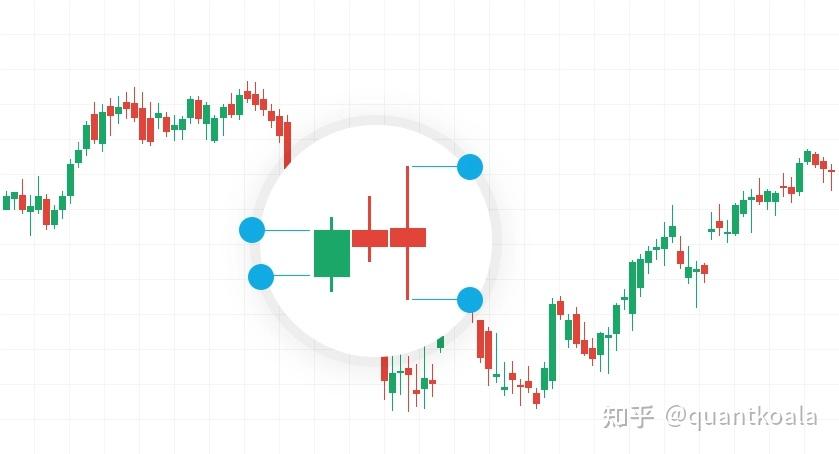
假设我们已经有了相对靠谱的阻力位和支撑位,那应该怎么使用呢?像上下轨突破策略那样使用吗?
可以换一个思路,这就是RSRS的创新点所在,不直接使用阻力位和支撑位这种绝对阈值方式,改为使用相对强度的方式。
就好比是,绝对阈值方式就是预测清华北大的学生能否将来年入百万千万,相对强度方式则是预测清华北大的学生收入将来是否超越双非院校的学生,这两者都不是绝对事件,但两者的预测难易程度一目了然,这个比方不是很恰当,是我能想到的最好的了,只是用来说明,让大伙儿更好地体会(惶恐狗头保命状ing)。

2.RSRS斜率指标和策略
现在说清楚了阻力位和支撑位的代理变量,和指标构建的核心思想,那再来唠唠RSRS的具体计算步骤和细节。

首先,获取N日最高价和最低价的价格序列,然后,对最高价和最低价序列进行最小二乘法
(OLS)线性回归,每日滚动进行,其中beta值就是斜率。
最高价 = alpha + beta×最低价
其中斜率值beta表示最高价相对最低价位置变化的程度,也就是说,当最低价变化为1的时候,最高价变动多少。
当斜率值beta很大时,支撑强度大于阻力强度,从图形上看就是,最高价的变动速度比最低价的要快,阻力逐渐减小,上涨空间大。

当斜率值beta很小时,阻力强度大于支撑强度,从图形上看就是,最高价的变动速度比最低价的要慢,上涨逐渐减缓,势头受阻见顶。

最后,这个斜率值beta就会被作为当日的RSRS值,确切来说应该是“RSRS斜率指标值”,因为后文会对指标不断改进,RSRS的含义会更加多样丰富。
RSRS的计算步骤和流程说完了,光说不练假把式,咱撸起袖子开干吧,从数据获取、指标计算和策略构建全部用代码实现和展示。
第一步,对照原版研报,获取沪深300指数从2005年至今的开高低收行情数据,这里使用的是股票量化开源库qstock,“pip install qstock”安装后,基本的功能无需注册便可以使用,萌新使用起来也非常丝滑。
import qstock as qs
# 获取沪深300指数从2005年至今的高开低收等行情数据,index是日期
data = qs.get_data(code_list=['HS300'], start='20050101', freq='d')[['open','high','low','close']]
# 删除名称列、排序并去除空值
data = data.sort_index().fillna(method='ffill').dropna()
# 插入日期列
data.insert(0, 'date', data.index)
# 将日期从datetime格式转换为str格式
data['date'] = data['date'].apply(lambda x: x.strftime('%Y-%m-%d'))
# 按收盘价计算每日涨幅
data['pct'] = data['close'] / data['close'].shift(1) - 1.0
data = data.dropna().reset_index(drop=True)
print(data.head(5))
print(data.tail(5))

第二步,这里的关键是计算每一日的斜率值beta,这里先给量化萌新说一个简单具体的例子,懂最小二乘法OLS的小伙伴可跳过。
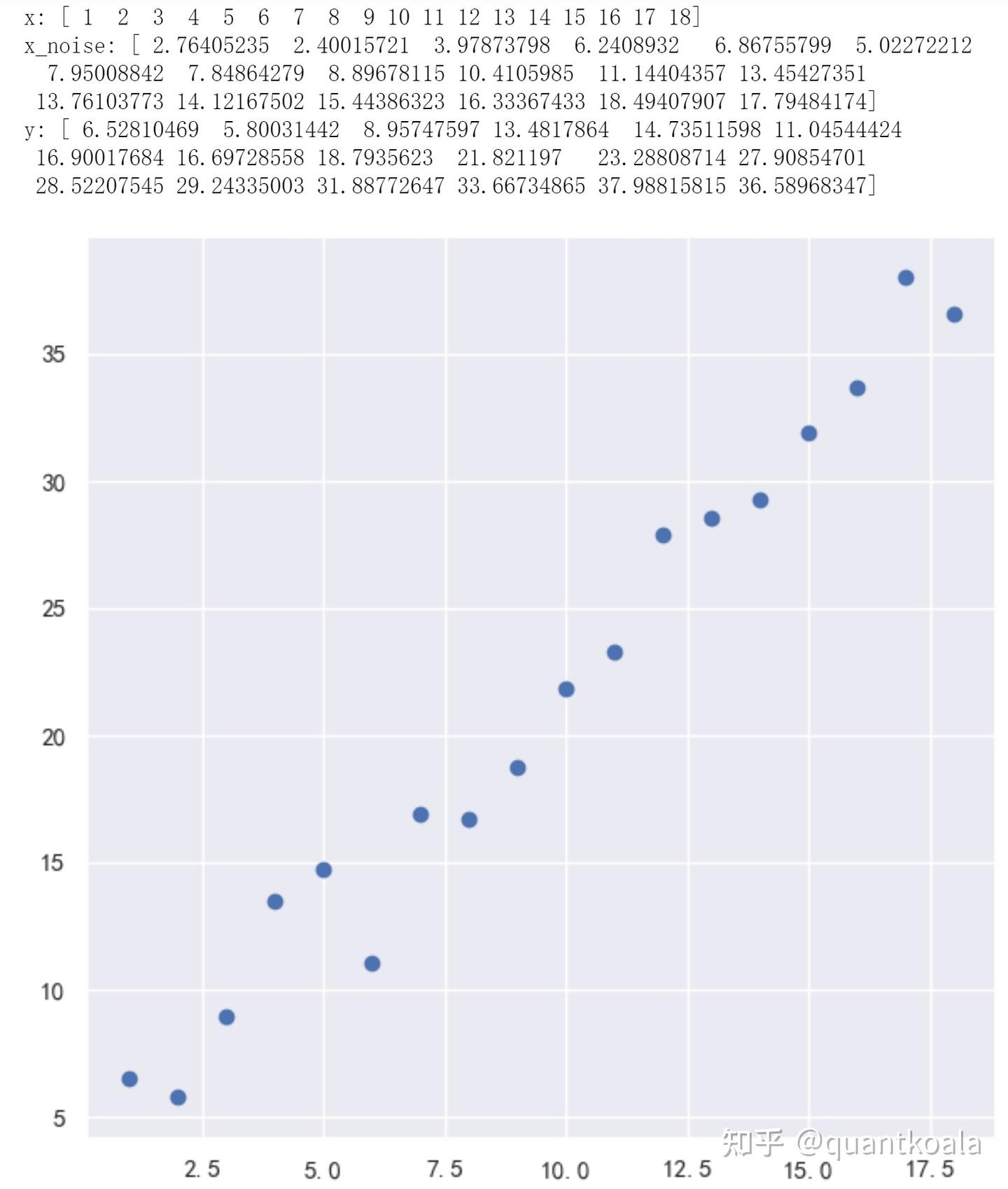
假设有18个二维的数据点,横轴X轴的坐标是1~18的等差数列,纵轴Y轴的坐标依照y=2*x_noise+1生成,x_noise是在横坐标x的基础上加入了随机数噪声,在这里,X轴数值对应的就是RSRS计算中的最低价,Y轴对应的就是最高价,具体分布如下。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
np.random.seed(0) #保证随机数生成的一致性
N = 18 #数据点个数
x = np.arange(1, N+1)
x_noise = x + np.random.randn(N) #加入随机数噪声干扰
y = 2 * x_noise + 1
print('x:', x)
print('x_noise:', x_noise)
print('y:', y)
plt.figure(figsize=(7,7))
plt.scatter(x, y)
plt.show()
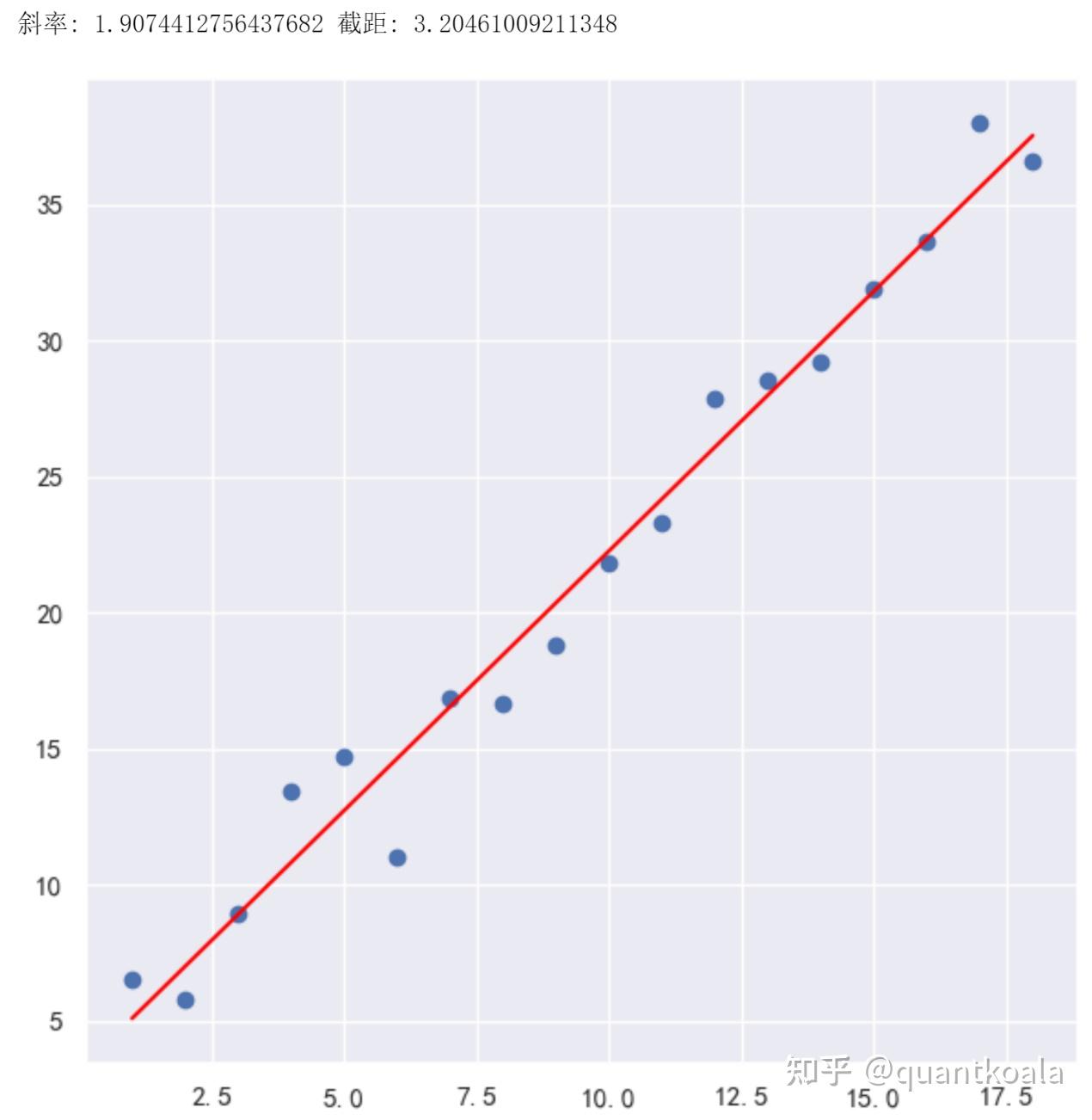
虽然有噪声的干扰,咱都知道它们的底层关系就是一条二维直线y=beta*x+alpha,其中beta=2是斜率,alpha=1是截距,最小二乘法OLS的作用就是根据已知的坐标数值,计算出斜率和截距。
在这里为了方(tou)便(lan),咱还是直接从Python免费机器学习库Scikit-learn
(简称sklearn)中导入LinearRegression求解,这里要注意的是,训练集必须是二维数组(矩阵)的形式,也就是每个样本对应的是一个向量,即使这个向量只有一个数值,这里使用reshape函数快速将n维向量转换为n x 1维矩阵。从最终结果看出,解出来的斜率为1.907,跟实际值还是非常接近的。
from sklearn.linear_model import LinearRegression
lr = LinearRegression().fit(x.reshape(-1, 1), y)
y_pred = lr.predict(x.reshape(-1, 1))
beta = lr.coef_[0]
alpha = lr.intercept_
print('斜率:', beta, '截距:', alpha)
plt.figure(figsize=(7,7))
plt.scatter(x, y)
plt.plot(x, y_pred, color='red')
plt.show()
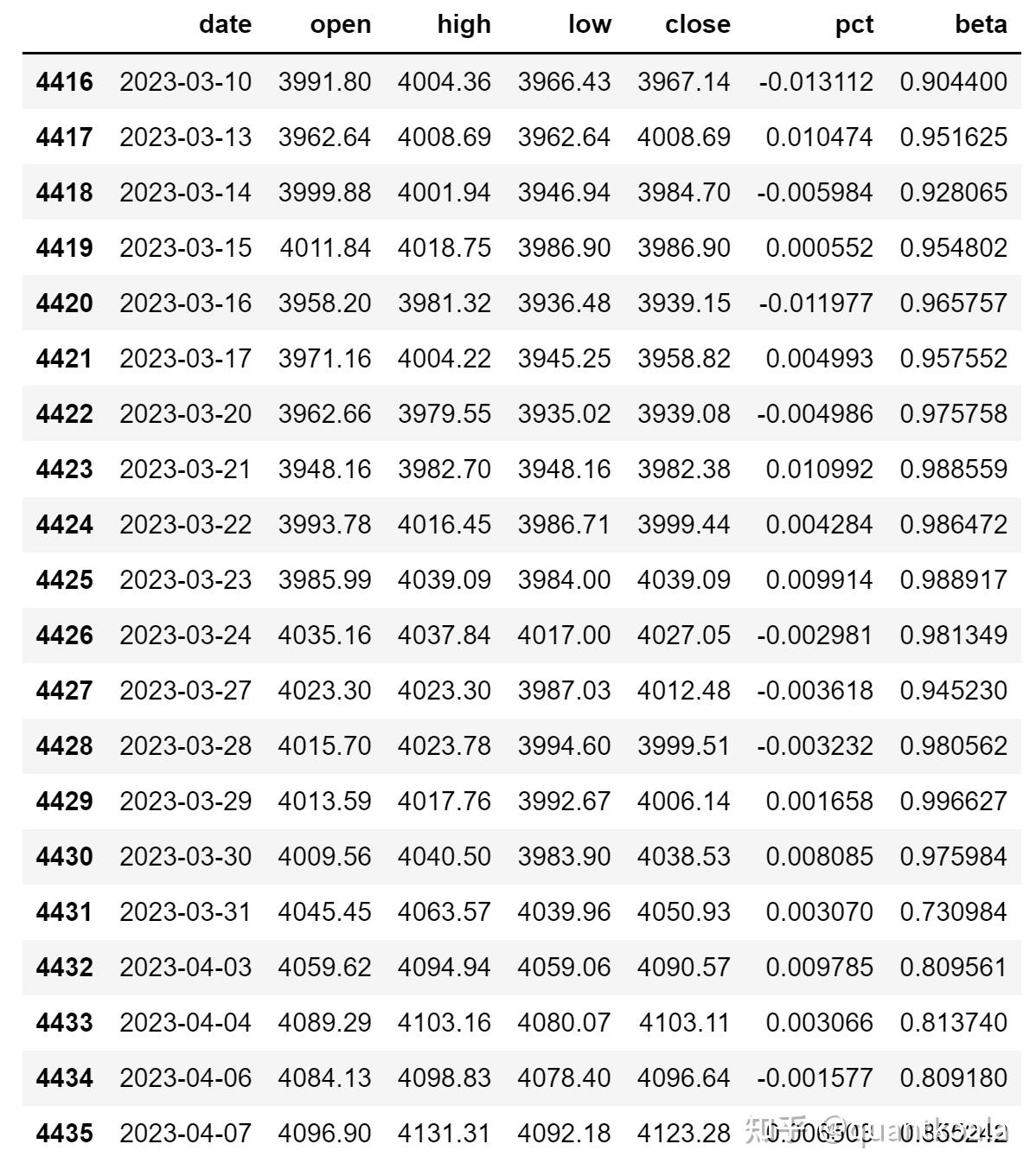
解单个序列的斜率值咱搞定了,在沪深300指数的行情数据上,咱只需要每个交易日滑动(rolling)计算18个交易日最高价vs最低价的斜率就可以了,为什么N=18呢,因为这是原版研报中在2017年定的最优参数,本期文章以复现为主,因此尊重历史客观事实按照原始参数。
def calculate_beta(df, window=18):
if df.shape[0] < window:
return np.nan
x = df['low'].values
y = df['high'].values
beta = LinearRegression().fit(x.reshape(-1, 1), y).coef_[0]
return beta
N = 18 #计算斜率时的数据点个数
data['beta'] = [calculate_beta(df,window=N) for df in data.rolling(N)]
data.tail(20)
现在咱们有了历史上每个交易日的beta值,也就是RSRS值,在这第三步里就可以构建针对大盘沪深300指数的量化择时策略了,这个策略的逻辑非常简单,就是“RSRS值大于1.0的时候,买入持有;RSRS值小于0.8,卖出平仓”,现实当中对应的交易标的可以是300ETF或IF股指期货。
有的小伙伴可能会好奇,为什么买入阈值是1.0、卖出阈值是0.8呢?原文当中的确定方法是,根据RSRS均值加减一个标准差形成的。
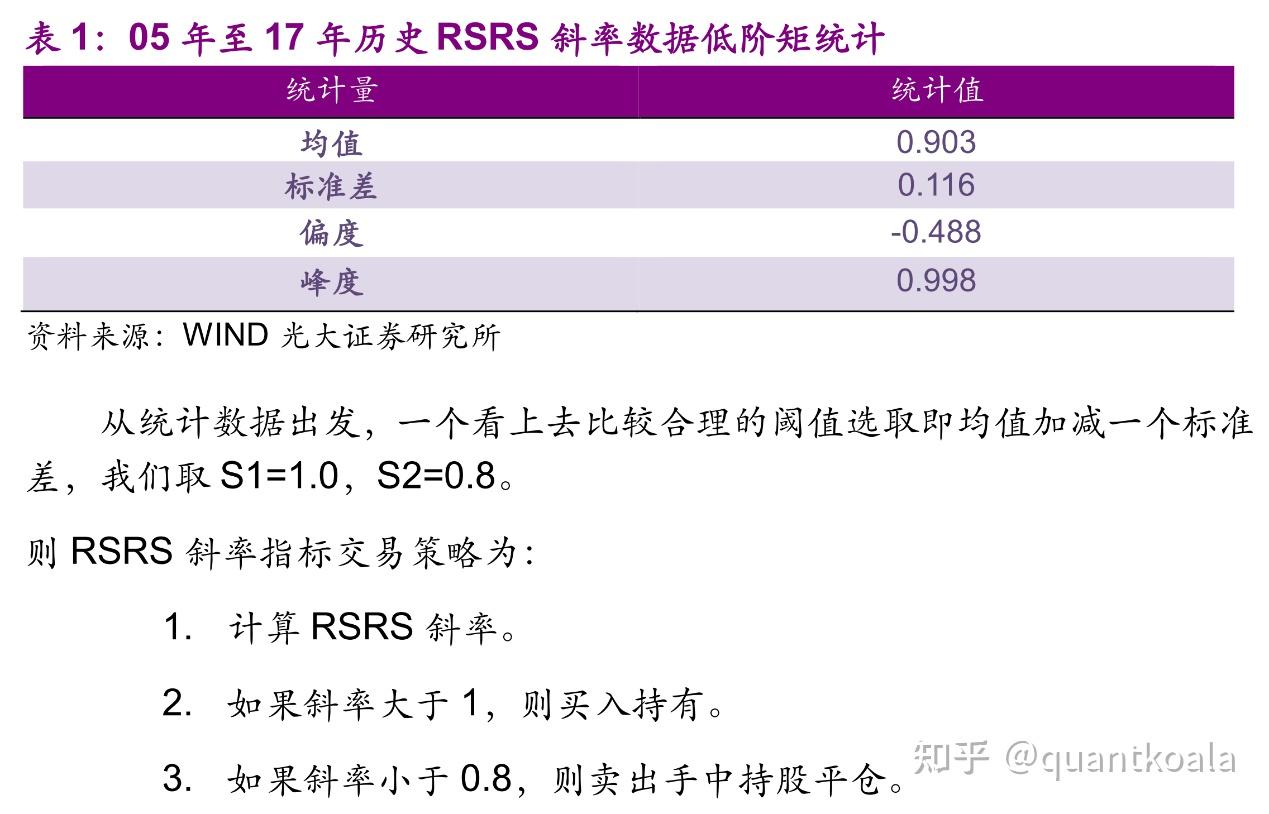
重新统计一下目前的数据,统计值和斜率分布如下,发现RSRS均值还是在0.9左右,标准差也还是在0.1左右,故买入阈值仍然可以定为1.0,卖出阈值定为0.8。
print('均值:%.3f' %data['beta'].mean())
print('标准差:%.3f' %data['beta'].std())
print('偏度:%.3f' %data['beta'].skew())
print('峰度:%.3f' %data['beta'].kurt())
y = list(range(200))
plt.figure(figsize=(16,8))
plt.hist(data['beta'], bins=100)
plt.plot(len(y)*[0.8], y, color='green', linestyle=':')
plt.plot(len(y)*[1.0], y, color='red', linestyle=':')
plt.show()
参考:https://zhuanlan.zhihu.com/p/620876365

